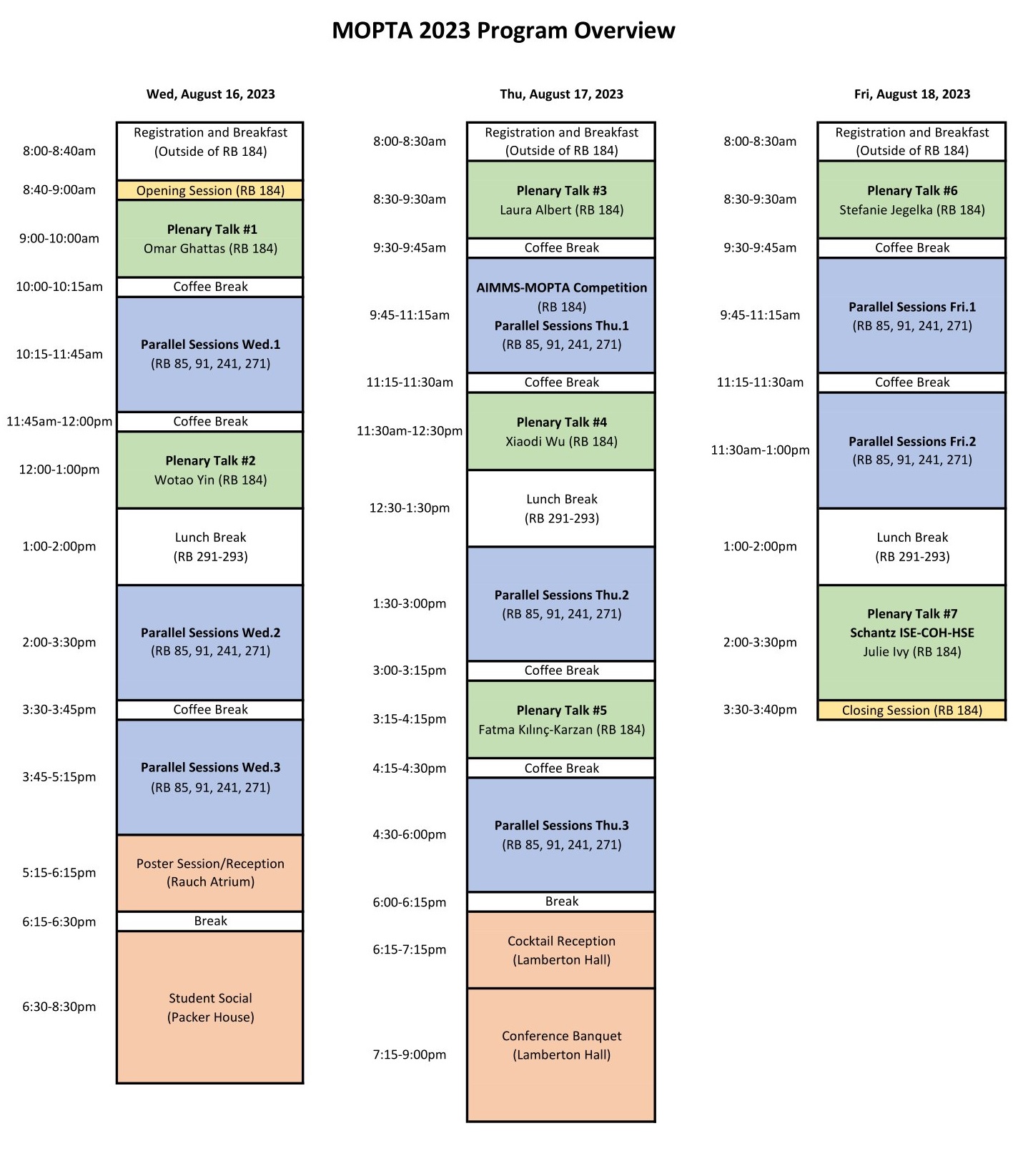
Conference program
Program
All technical sessions, registration, breakfast, and lunch take place at
Rauch Business Center
621 Taylor Street, Bethlehem, PA 18015
Program overview can be downloaded here.
Session overview can be downloaded here.
Select the image below to download the MOPTA 2023 Program Book
Last updated: August 13, 2023

Daily Schedule
Wednesday Thursday Friday